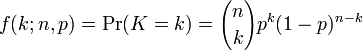What I did during AndroidConf Brasil 2011

Hey, reader! 

Today I was in the AndroidConf Brasil 2011 with some fellows. 

It was a good event. Not the best, nor the worst. A good one.

People who know me, know that I don't like cellphones. Then, since I'm not a proper example of enthusiastic about this topic, I tried to invest my time with an experiment. 

Last days I was trying to minify a javascript file by myself. I thought that would be as easily as count till 3. It turns out that I was wrong. I had to write a compiler in order to make it work well. Thus, I went back to the theory to see how it could help me.

As I was reading about automata and its uses, it turned out to be interesting to have a working example of the theory I was dealing with. And why not during the event? 

First presentation: git init. No wireless network?! That's ok. Thank you git!

There I was, writing a simple Deterministic Finite Automaton. 

Had a lot of fun doing that. 

Great saturday, =)

If you wanna see the resulting code -> https://github.com/cathoderay/dfa.

Need some rest now.

Till the next post!

Ronald Kaiser

Slowing down

Nowadays, we all live in a fast-paced world.
Most of us live in a non-stop multitasking mode, trying to think in everything in advance, planning and predicting the future at all costs. Living in the future.

I want to slow down.

Sometimes we just run, without enjoying life.
Sometimes we don't stop to realize what we have just accomplished, what are we and how beautiful is life.

Slowing down.

Poisson distribution -- part 1

I was presented to this topic under my computer science classes at university, but I didn't get much intuition, though I wanted to.

The Poisson distribution can be observed in many situations in life and that's why I'd like to understand it better. It was first published in 1838 by Siméon-Denis Poisson in his book Recherches sur la probabilité des jugements en matière criminelle et en matière civile (this link really made me think to learn more french). As any statistical distribution, the Poisson one is a function that returns the probability of some event. No mistery till now. But what this formula

tries to absorb from the real world and why should worth knowing?

Let's begin with something simple. Imagine situations that happen randomly -- or can be dealt as so -- and must assume 2 distinct values. For example, the classical flip of a coin or the "waking up early" event.

Assuming that "waking up early" is an impredictable event -- and I think is reasonably to think like that --, what is the probability of waking up early exactly 20 days of a month?

We can model the situation representing the success and fails in a string of 30 "houses" -- mapping each day of a month -- containing either an S or an F, and attaching a probability p for each success. For example:

SSFSFSSSSSSSFSFSFSSSFSFSSSFSFS

So, what's the probability of waking up early 20 days in a 30 day month?

Let's break the problem.

By the fundamental axioms, the sum of probabilites must sum up to 1. Given that, the probability of failures is equivalent to (1 - p). Assuming that waking up early today is independent from waking up early yesterday, the probability of the event SSFSFSSSSSSSFSFSFSSSFSFSSSFSFS is, thus, p²⁰(1-p)¹⁰.

Finished, right? Wrong!

We have 30 days to wake up. Waking up early 20 days of 30 can be accomplished in many ways. SSFSFSSSSSSSFSFSFSSSFSFSSSFSFS is just a single case in which we failed to waking up early days 3, 5, 13, 15, 17, 21, 23, 27, 29. In order to calculate the final probability, we must know how many ways we can take 20 from 30. This smells like combinations formula. Do you remember it? Personally, I don't like to think in terms of Combinations and Permutations, they're just nouns for the same underlying idea, the fundamental counting principle (I intend to write a post about it some day).

The number of ways we can take 20 from 30 is given by 30!/(20!10!). The same result can be reached using the Pascal Triangle. So, the final probability is given by:

30!/(20!10!)p²⁰(1-p)¹⁰ = 30045015p²⁰(1-p)¹⁰

If we wanted to know the probability of waking up early k days within n days, giving that the success probability is still p, we could simply apply the more general binomial distribution:

In the next post, I'll explain the relationship between Binomial, Poisson distributions and possibly datacenter monitoring.

Till the next one!

pomodoro technique with arduino experiment

Today I decided to implement the pomodoro technique with my arduino.

It turns on an orange led (I didn't have a red one) from 10 to 10 seconds, just to remember me that I'm in a busy time, while a tic tac is reproduced by the buzzer.

After the first 25 minutes -- suggestion by Francesco Cirillo, the author of the pomodoro technique -- an alarm is activated. Then, a green led is turned on for 5 minutes -- so, I can rest a bit -- and the loop continues.

It's working pretty well, =)

The source code is available at my github -> https://github.com/cathoderay/pomoino/blob/master/pomoino.pde

Till the next experiment =)

Ronald Kaiser