
I was presented to this topic under my computer science classes at university, but I didn't get much intuition, though I wanted to.
The Poisson distribution can be observed in many situations in life and that's why I'd like to understand it better. It was first published in 1838 by Siméon-Denis Poisson in his book Recherches sur la probabilité des jugements en matière criminelle et en matière civile (this link really made me think to learn more french). As any statistical distribution, the Poisson one is a function that returns the probability of some event. No mistery till now. But what this formula

tries to absorb from the real world and why should worth knowing?
Let's begin with something simple. Imagine situations that happen randomly -- or can be dealt as so -- and must assume 2 distinct values. For example, the classical flip of a coin or the "waking up early" event.

Assuming that "waking up early" is an impredictable event -- and I think is reasonably to think like that --, what is the probability of waking up early exactly 20 days of a month?
We can model the situation representing the success and fails in a string of 30 "houses" -- mapping each day of a month -- containing either an S or an F, and attaching a probability p for each success. For example:
SSFSFSSSSSSSFSFSFSSSFSFSSSFSFS
So, what's the probability of waking up early 20 days in a 30 day month?
Let's break the problem.
By the fundamental axioms, the sum of probabilites must sum up to 1. Given that, the probability of failures is equivalent to (1 - p). Assuming that waking up early today is independent from waking up early yesterday, the probability of the event SSFSFSSSSSSSFSFSFSSSFSFSSSFSFS is, thus, p20(1-p)10.
Finished, right? Wrong!
We have 30 days to wake up. Waking up early 20 days of 30 can be accomplished in many ways. SSFSFSSSSSSSFSFSFSSSFSFSSSFSFS is just a single case in which we failed to waking up early days 3, 5, 13, 15, 17, 21, 23, 27, 29. In order to calculate the final probability, we must know how many ways we can take 20 from 30. This smells like combinations formula. Do you remember it? Personally, I don't like to think in terms of Combinations and Permutations, they're just nouns for the same underlying idea, the fundamental counting principle (I intend to write a post about it some day).
The number of ways we can take 20 from 30 is given by 30!/(20!10!). The same result can be reached using the Pascal Triangle. So, the final probability is given by:
30!/(20!10!)p20(1-p)10 = 30045015p20(1-p)10
If we wanted to know the probability of waking up early k days within n days, giving that the success probability is still p, we could simply apply the more general binomial distribution:
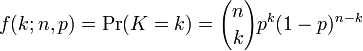
In the next post, I'll explain the relationship between Binomial, Poisson distributions and possibly datacenter monitoring.
Till the next one!
I honestly thought i'd never read about that again in my life.
ReplyDeleteToo late now. But it isn't so bad when i a)actually understand it and b)don't have to study for a test =D
Very good!
ReplyDelete